Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
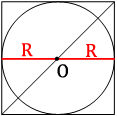Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*22√2=44√2
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(44√2)2
b2=2*442*2
b2=442*22=(44*2)2=882
b=88
Ответ: 88
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Хочу получать новые решения
Ни какого спама
(«простой»), должен быть выпуклым.
Автор: Таська
Комментарии: