Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Вариант №1 (Предложил пользователь Людмила)
По второму свойству вписанной в четырехугольник окружности:
AB+CD=BC+AD
7+14=10+AD
AD=7+14-10=11
Ответ: 11
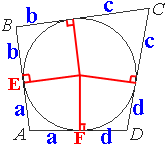AB и AD - это
касательные к окружности.Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 8√
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Хочу получать новые решения
Ни какого спама
(«простой»), должен быть выпуклым.
Автор: Таська
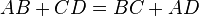
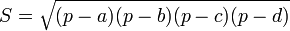
Комментарии:
(2017-05-14 20:24:54) Администратор: Людмила, спасибо большое за Ваше решение. Опубликовано от Вашего имени.
(2017-05-13 18:58:46) Людмила: Можно использовать теорему о том, что окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны. AB+CD=BC+AD, 7+14=10+AD