
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ684 –Є–Ј 1087 |
 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –њ–µ—А–Є–Љ–µ—В—А –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є –Њ–і–љ–∞ –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 6.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –њ–µ—А–Є–Љ–µ—В—А –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є –Њ–і–љ–∞ –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 6.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –Љ–Њ–ґ–µ—В –±—Л—В—М –≤–њ–Є—Б–∞–љ–∞ –≤ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї, –Ї–Њ–≥–і–∞ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П
—Г—Б–ї–Њ–≤–Є–µ:
AB+CD=BC+AD
AB=CD=x (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞)
BC=AD=y (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞)
–Я–Њ–ї—Г—З–∞–µ–Љ:
x+x=y+y
2x=2y
x=y, —В.–µ. –≤—Б–µ —Б—В–Њ—А–Њ–љ—Л –љ–∞—И–µ–≥–Њ
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ—Л, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Н—В–Њ
—А–Њ–Љ–±.
–Я–µ—А–Є–Љ–µ—В—А
—А–Њ–Љ–±–∞ —А–∞–≤–µ–љ:
P=6*4=24
–Ю—В–≤–µ—В: 24
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AB=24, AC=21, MN=14. –Э–∞–є–і–Є—В–µ AM.
–Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AB=24, AC=21, MN=14. –Э–∞–є–і–Є—В–µ AM.
 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –њ—А–Њ–≤–µ–і–µ–љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М AC. –Ґ–Њ—З–Ї–∞ O —П–≤–ї—П–µ—В—Б—П —Ж–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC. –†–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —В–Њ—З–Ї–Є O –і–Њ —В–Њ—З–Ї–Є A –Є –њ—А—П–Љ—Л—Е AD –Є AC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л 25, 8 –Є 7. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –њ—А–Њ–≤–µ–і–µ–љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М AC. –Ґ–Њ—З–Ї–∞ O —П–≤–ї—П–µ—В—Б—П —Ж–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC. –†–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —В–Њ—З–Ї–Є O –і–Њ —В–Њ—З–Ї–Є A –Є –њ—А—П–Љ—Л—Е AD –Є AC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л 25, 8 –Є 7. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD.
–Ю—Б–љ–Њ–≤–∞–љ–Є–µ AC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–Њ 6. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —А–∞–і–Є—Г—Б–∞ 4,5 —Б —Ж–µ–љ—В—А–Њ–Љ –≤–љ–µ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ї–∞—Б–∞–µ—В—Б—П –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є—П –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Є –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є—П AC –≤ –µ–≥–Њ —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
 –°—В–Њ—А–Њ–љ–∞ AB –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AD.
–Ґ–Њ—З–Ї–∞ L вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ DL вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞
—Г–≥–ї–∞ ADC.
–°—В–Њ—А–Њ–љ–∞ AB –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AD.
–Ґ–Њ—З–Ї–∞ L вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ DL вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞
—Г–≥–ї–∞ ADC.
–Ъ–∞–Ї–Є–µ –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л?
1) –Ф–ї—П —В–Њ—З–Ї–Є, –ї–µ–ґ–∞—Й–µ–є –љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —А–∞—Б—Б—В–Њ—П–љ–Є–µ –і–Њ —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ —А–∞–і–Є—Г—Б—Г.
2) –Я–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—О –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є –љ–∞ –≤—Л—Б–Њ—В—Г.
3) –Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 1, 2, 4 –љ–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В.
–Т –Њ—В–≤–µ—В –Ј–∞–њ–Є—И–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤—Л–±—А–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –±–µ–Ј –њ—А–Њ–±–µ–ї–Њ–≤, –Ј–∞–њ—П—В—Л—Е –Є –і—А—Г–≥–Є—Е –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Б–Є–Љ–≤–Њ–ї–Њ–≤.
 (¬Ђ–њ—А–Њ—Б—В–Њ–є¬ї), –і–Њ–ї–ґ–µ–љ –±—Л—В—М –≤—Л–њ—Г–Ї–ї—Л–Љ.
(¬Ђ–њ—А–Њ—Б—В–Њ–є¬ї), –і–Њ–ї–ґ–µ–љ –±—Л—В—М –≤—Л–њ—Г–Ї–ї—Л–Љ.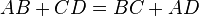
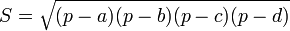
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2016-05-23 21:05:51) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–ї–µ–љ–∞, —Б—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞, –њ–Њ —Г—Б–ї–Њ–≤–Є—О, —А–∞–≤–љ–∞ 6, –њ–Њ—Н—В–Њ–Љ—Г 4*6, –љ—Г –Є–ї–Є 6*4. –І—В–Њ–±—Л –љ–µ –±—Л–ї–Њ —А–∞–Ј–љ–Њ—З—В–µ–љ–Є–є, —П –њ–Њ–Љ–µ–љ—П–ї –њ–Њ—А—П–і–Њ–Ї –Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є.
(2016-05-23 11:01:33) –Х–ї–µ–љ–∞: –Я–Њ—З–µ–Љ—Г –њ–µ—А–Є–Љ–µ—В—А —А–Њ–Љ–±–∞ —А–∞–≤–µ–љ 4*6? –Ф–Њ–ї–ґ–љ–Њ –±—Л—В—М 4*4.