X
пїњ
–°–≤–Њ–є—Б—В–≤–∞ –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є:
1) –Т –Ї–∞–ґ–і—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –њ—А–Є—В–Њ–Љ —В–Њ–ї—М–Ї–Њ –Њ–і–љ—Г.
2) –¶–µ–љ—В—А I –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Є–љ—Ж–µ–љ—В—А–Њ–Љ, –Њ–љ —А–∞–≤–љ–Њ—Г–і–∞–ї—С–љ –Њ—В –≤—Б–µ—Е —Б—В–Њ—А–Њ–љ –Є —П–≤–ї—П–µ—В—Б—П —В–Њ—З–Ї–Њ–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
3) –†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ:
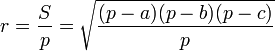
.
4) –Х—Б–ї–Є AB вАФ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, —В–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –Ї–∞—Б–∞—О—Й–∞—П—Б—П —Б—В–Њ—А–Њ–љ —Г–≥–ї–∞ ACB –≤ —В–Њ—З–Ї–∞—Е A –Є B, –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –Є–љ—Ж–µ–љ—В—А —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
5) –§–Њ—А–Љ—Г–ї–∞ –≠–є–ї–µ—А–∞: R
2-2Rr=|OI|
2, –≥–і–µ R вАФ —А–∞–і–Є—Г—Б –Њ–њ–Є—Б–∞–љ–љ–Њ–є –≤–Њ–Ї—А—Г–≥ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, r вАФ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –љ–µ–≥–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, O вАФ —Ж–µ–љ—В—А –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, I вАФ —Ж–µ–љ—В—А –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
6) –Х—Б–ї–Є –њ—А—П–Љ–∞—П, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј —В–Њ—З–Ї—Г I –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ —Б—В–Њ—А–Њ–љ–µ AB, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л BC –Є CA –≤ —В–Њ—З–Ї–∞—Е A
1 –Є B
1, —В–Њ A
1B
1=A
1B + AB
1.
7) –Ґ–Њ—З–Ї–Є –Ї–∞—Б–∞–љ–Є—П –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї T –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б–Њ–µ–і–Є–љ–µ–љ—Л –Њ—В—А–µ–Ј–Ї–∞–Љ–Є вАФ –њ–Њ–ї—Г—З–∞–µ—В—Б—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї T
1.
7.1) –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л T —П–≤–ї—П—О—В—Б—П —Б–µ—А–µ–і–Є–љ–љ—Л–Љ–Є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–∞–Љ–Є T
1.
7.2) –Я—Г—Б—В—М T
2 вАФ –Њ—А—В–Њ—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї T
1. –Ґ–Њ–≥–і–∞ –µ–≥–Њ —Б—В–Њ—А–Њ–љ—Л –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л —Б—В–Њ—А–Њ–љ–∞–Љ –Є—Б—Е–Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ T.
7.3) –Я—Г—Б—В—М T
3 вАФ —Б–µ—А–µ–і–Є–љ–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї T
1. –Ґ–Њ–≥–і–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л T —П–≤–ї—П—О—В—Б—П –≤—Л—Б–Њ—В–∞–Љ–Є T
3.
7.4) –Я—Г—Б—В—М T
4 вАФ –Њ—А—В–Њ—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї T
3, —В–Њ–≥–і–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л T —П–≤–ї—П—О—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞–Љ–Є T
4.
8) –†–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —Б –Ї–∞—В–µ—В–∞–Љ–Є a, b –Є –≥–Є–њ–Њ—В–µ–љ—Г–Ј–Њ–є c –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ:
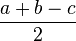
9) –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –≤–µ—А—И–Є–љ—Л –° —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–Њ —В–Њ—З–Ї–Є, –≤ –Ї–Њ—В–Њ—А–Њ–є –≤–њ–Є—Б–∞–љ–љ–∞—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –Ї–∞—Б–∞–µ—В—Б—П —Б—В–Њ—А–Њ–љ—Л, —А–∞–≤–љ–Њ:
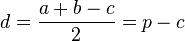
10) –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –≤–µ—А—И–Є–љ—Л C –і–Њ —Ж–µ–љ—В—А–∞ –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ:
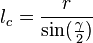
–≥–і–µ r вАФ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –∞ –≥–∞–Љ–Љ–∞ вАФ —Г–≥–Њ–ї –≤–µ—А—И–Є–љ—Л C.
11) –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –≤–µ—А—И–Є–љ—Л C –і–Њ —Ж–µ–љ—В—А–∞ –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Љ–Њ–ґ–µ—В —В–∞–Ї–ґ–µ –±—Л—В—М –љ–∞–є–і–µ–љ–Њ –њ–Њ —Д–Њ—А–Љ—Г–ї–∞–Љ:
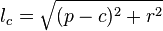
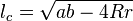
12) –Ґ–µ–Њ—А–µ–Љ–∞ –Њ —В—А–µ–Ј—Г–±—Ж–µ –Є–ї–Є –Њ —В—А–Є–ї–Є—Б—В–љ–Є–Ї–µ: –Х—Б–ї–Є W вАФ —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–∞ A —Б –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М—О, –∞ I вАФ —Ж–µ–љ—В—А –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —В–Њ |WI|=|WB|=|WC|.
13) –Ы–µ–Љ–Љ–∞ –Т–µ—А—А—М–µ—А–∞: –њ—Г—Б—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М V –Ї–∞—Б–∞–µ—В—Б—П —Б—В–Њ—А–Њ–љ AB, AC –Є –і—Г–≥–Є BC –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Ґ–Њ–≥–і–∞ —В–Њ—З–Ї–Є –Ї–∞—Б–∞–љ–Є—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є V —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є –Є —Ж–µ–љ—В—А –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –ї–µ–ґ–∞—В –љ–∞ –Њ–і–љ–Њ–є –њ—А—П–Љ–Њ–є.

 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞ –Я–µ—А–Є–Љ–µ—В—А —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–µ–љ 54, –Њ–і–љ–∞ –Є–Ј —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 15,
–∞ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –љ–µ–≥–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 1. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Я–µ—А–Є–Љ–µ—В—А —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–µ–љ 54, –Њ–і–љ–∞ –Є–Ј —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 15,
–∞ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –љ–µ–≥–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 1. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 45¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 45¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –Њ–±—А–∞–Ј—Г—О—В –Љ–Є–љ—Г—В–љ–∞—П –Є —З–∞—Б–Њ–≤–∞—П —Б—В—А–µ–ї–Ї–Є —З–∞—Б–Њ–≤ –≤ 11:00. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –Њ–±—А–∞–Ј—Г—О—В –Љ–Є–љ—Г—В–љ–∞—П –Є —З–∞—Б–Њ–≤–∞—П —Б—В—А–µ–ї–Ї–Є —З–∞—Б–Њ–≤ –≤ 11:00. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.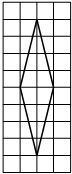 –Э–∞ –Ї–ї–µ—В—З–∞—В–Њ–є –±—Г–Љ–∞–≥–µ —Б —А–∞–Ј–Љ–µ—А–Њ–Љ –Ї–ї–µ—В–Ї–Є 1x1 –Є–Ј–Њ–±—А–∞–ґ—С–љ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —А–Њ–Љ–±–∞.
–Э–∞ –Ї–ї–µ—В—З–∞—В–Њ–є –±—Г–Љ–∞–≥–µ —Б —А–∞–Ј–Љ–µ—А–Њ–Љ –Ї–ї–µ—В–Ї–Є 1x1 –Є–Ј–Њ–±—А–∞–ґ—С–љ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —А–Њ–Љ–±–∞. –Я–ї–Њ—Й–∞–і—М —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 1600√
–Я–ї–Њ—Й–∞–і—М —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 1600√ –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ –Ї–≤–∞–і—А–∞—В–∞, —А–∞–≤–µ–љ 14√
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ –Ї–≤–∞–і—А–∞—В–∞, —А–∞–≤–µ–љ 14√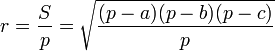 .
.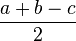
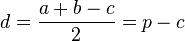
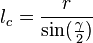
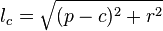
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2022-12-27 19:06:59) –Р–ї–Є–љ–∞: –†–∞–і–Є–Њ—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О —А–∞–≤–µ–љ 14 –љ–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є
(2018-03-04 17:21:28) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–∞ –Њ–љ–∞ –љ–µ –љ—Г–ґ–љ–∞. –Ю–±—Л—З–љ–Њ, –∞–≤—В–Њ—А—Л –і–ї—П –Њ–і–љ–Њ–≥–Њ –Є —В–Њ–≥–Њ –ґ–µ —Г—Б–ї–Њ–≤–Є—П –њ—А–Є–і—Г–Љ—Л–≤–∞—О—В —А–∞–Ј–ї–Є—З–љ—Л–µ –≤–Њ–њ—А–Њ—Б—Л. –Я–Њ—Н—В–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є–µ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –±–Њ–ї–µ–µ —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ—Л–Љ –Є —Б –Є–Ј–±—Л—В–Њ—З–љ—Л–Љ–Є –і–∞–љ–љ—Л–Љ–Є.
(2018-03-03 22:54:08) : –Ч–∞—З–µ–Љ –љ—Г–ґ–љ–∞ –±—Л–ї–∞ —Б—В–Њ—А–Њ–љ–∞ 15