Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=18, DK=9, BC=16. Найдите AD.
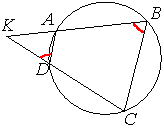По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA - является
смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.
Рассмотрим треугольникик AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC, это мы определили ранее.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(9*16)/18=16/2=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Площадь равнобедренного треугольника равна 196√
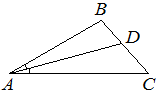В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
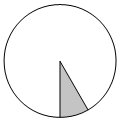Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-11-19 12:43:29) Дианна: Четырехугольник АВСD (AB>BC) вписан в окружность . известно что АD=СD. докажите что биссектриса угла АDВ отсекает от угла ВАС равнобедренный треугольник
(2022-11-19 12:42:58) : Четырехугольник АВСD (AB>BC) вписан в окружность . известно что АD=СD. докажите что биссектриса угла АDВ отсекает от угла ВАС равнобедренный треугольник