
 Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=21+8=29 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора: AD2=AH2+DH2
292=AH2+212
841=AH2+441
AH2=400
AH=20
Ответ: AH=20
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
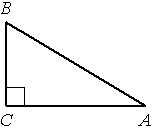 В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
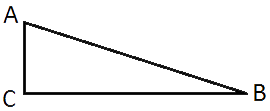 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
 В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Комментарии:
(2017-02-20 23:56:06) Администратор: Наталья, для этого и трудимся. Спасибо и Вам.
(2017-02-20 23:15:17) Наталья: Замечательный сайт, в геометрии не сильно шарю а в этом году огэ сдавать ваш сайт стал для меня находкой, очень подробно и понятно всё объясняется ❤
(2015-02-21 12:32:03) Администратор: Виктория, спасибо и Вам за теплые слова.
(2015-02-21 11:16:00) Виктория: Как замечательно, что существует этот сайт. Спасибо вам огромное)
(2014-12-12 20:31:53) Эбонит: норм
(2014-06-13 14:59:47) динара : спасибо