Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Так как сторона AC треугольника ABC проходит через центр
описанной около него окружности, то AC - это диаметр окружности.
Следовательно, треугольник ABC - прямоугольный (по
свойству описанной окружности), т.е. ∠B=90°.
По
теореме о сумме углов треугольника:
∠A+∠B+∠C=180°
81°+90°+∠C=180°
∠C=180°-81°-90°
∠C=9°
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
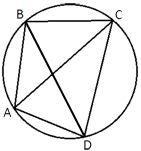Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
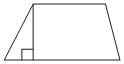Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: