
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ411 –Η–Ζ 1087 |
 –Δ–Ψ―΅–Κ–Α H ―è–≤–Μ―è–Β―²―¹―è –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ –≤―΄―¹–Ψ―²―΄ BH, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Ϋ–Ψ–Ι –Η–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α B –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC. –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ BH –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CB –≤ ―²–Ψ―΅–Κ–Α―Ö P –Η K ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β PK, –Β―¹–Μ–Η BH=16.
–Δ–Ψ―΅–Κ–Α H ―è–≤–Μ―è–Β―²―¹―è –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ –≤―΄―¹–Ψ―²―΄ BH, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Ϋ–Ψ–Ι –Η–Ζ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α B –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC. –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ BH –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CB –≤ ―²–Ψ―΅–Κ–Α―Ö P –Η K ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β PK, –Β―¹–Μ–Η BH=16.
–£–Α―Ä–Η–Α–Ϋ―² ⳕ1 (–ü―Ä–Η―¹–Μ–Α–Μ –Ψ–¥–Η–Ϋ –Η–Ζ –Ϋ–Α―à–Η―Ö –Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²–Β–Μ–Β–Ι, –Η–Φ―è –Ϋ–Β –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ).
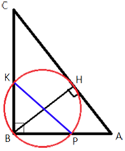 ∠KBP=90¬Α (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é)
∠KBP=90¬Α (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é)
–ü―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ KPB ―¹ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Ψ–Ι PK –≤–Ω–Η―¹–Α–Ϋ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, PK ―è–≤–Μ―è–Β―²―¹―è –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. (–Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ–± –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η).
KP=BH=16
–û―²–≤–Β―²: PK=16
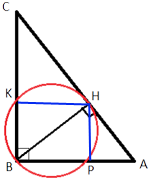 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η KH –Η HP.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η KH –Η HP.–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ
AOB ―Ä–Α–≤–Β–Ϋ 60¬Α. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―Ö–Ψ―Ä–¥―΄ AB, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä―É―é –Ψ–Ϋ –Ψ–Ω–Η―Ä–Α–Β―²―¹―è, –Β―¹–Μ–Η ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 5.
–Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ
AOB ―Ä–Α–≤–Β–Ϋ 60¬Α. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―Ö–Ψ―Ä–¥―΄ AB, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä―É―é –Ψ–Ϋ –Ψ–Ω–Η―Ä–Α–Β―²―¹―è, –Β―¹–Μ–Η ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 5.
 –€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –≤―²―Ä–Ψ–Β –±–Ψ–Μ―¨―à–Β –¥–Μ–Η–Ϋ―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
–€–Β–¥–Η–Α–Ϋ–Α BM –Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α AP ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –¥–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC –≤―²―Ä–Ψ–Β –±–Ψ–Μ―¨―à–Β –¥–Μ–Η–Ϋ―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α AKM –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
 –€–Β–¥–Η–Α–Ϋ–Α BM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―è–≤–Μ―è–Β―²―¹―è –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Β–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –≤ –Β―ë ―¹–Β―Ä–Β–¥–Η–Ϋ–Β. –î–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC ―Ä–Α–≤–Ϋ–Α 4. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–€–Β–¥–Η–Α–Ϋ–Α BM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―è–≤–Μ―è–Β―²―¹―è –¥–Η–Α–Φ–Β―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Β–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –≤ –Β―ë ―¹–Β―Ä–Β–¥–Η–Ϋ–Β. –î–Μ–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AC ―Ä–Α–≤–Ϋ–Α 4. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
 –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABC . –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABC . –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
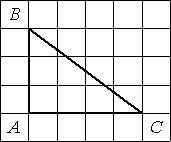 –ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α –Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α –Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.



–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: