Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
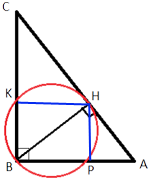Проведем отрезки KH и HP.
Треугольники BKH и BPH являются
вписанными в данную окружность. А т.к. центр этой окружности располагается на середине их стороны BH, то это означает, что эти треугольники прямоугольные с гипотенузой BH (по
свойству описанной окружности).
Следовательно, ∠HKB и ∠HPB - прямые.
Рассмотрим четырехугольник BKHP, сумма углов любого четырехугольника равна 360°, следовательно ∠HKB+∠KBP+∠HPB+∠PHK=360°
90°+90°+90°+∠PHK=360°
∠PHK=90°
То есть получается, что четырехугольник BKHP является
прямоугольником. Диагонали этого прямоугольника BH и PK.
PK=BH=13 (по свойству
прямоугольника)
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
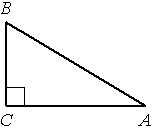В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=177°. Найдите величину угла BOC. Ответ дайте в градусах.
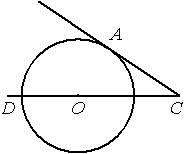Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: