
 Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
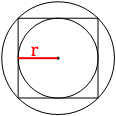 Проведем радиус
вписанной окружности, как на рисунке.
Проведем радиус
вписанной окружности, как на рисунке.
Очевидно, что r=a/2, где а - сторона
квадрата.
a=2r=2*24√2=48√2
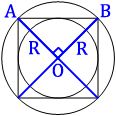 Проведем диаметры
описанной окружности, как показано на втором рисунке.
Проведем диаметры
описанной окружности, как показано на втором рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=OA2+OB2
a2=R2+R2
a2=2R2
(48√2)2=2R2
2304*2=2R2
2304=R2
R=√2304=48
Ответ: 48
Поделитесь решением
Присоединяйтесь к нам...
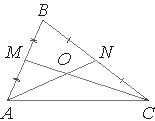 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
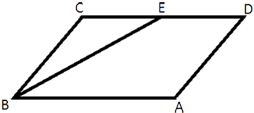 Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
 Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.



Комментарии:
(2024-02-11 17:36:43) лена: ттт