В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
Окружность может быть вписана в четырехугольник, когда выполняется
условие:
AB+CD=BC+AD
AB=CD=x (по
свойству параллелограмма)
BC=AD=y (по
свойству параллелограмма)
Получаем:
x+x=y+y
2x=2y
x=y, т.е. все стороны нашего
параллелограмма равны, следовательно это
ромб.
Периметр
ромба равен:
P=6*4=24
Ответ: 24
Поделитесь решением
Присоединяйтесь к нам...
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
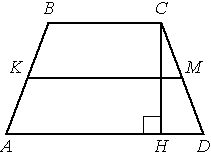В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-05-23 21:05:51) Администратор: Елена, сторона ромба, по условию, равна 6, поэтому 4*6, ну или 6*4. Чтобы не было разночтений, я поменял порядок множителей.
(2016-05-23 11:01:33) Елена: Почему периметр ромба равен 4*6? Должно быть 4*4.