
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
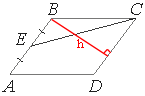 Проведем высоту
параллелограмма из угла ABC.
Проведем высоту
параллелограмма из угла ABC.
По первой формуле, площадь параллелограмма равна:
Sп=CD*h=28
h=28/CD
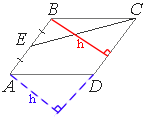 Высота параллелограмма является так же и высотой
трапеции, так как основания
трапеции и
параллелограмма лежат на одних и тех же прямых (AB и DC).
Высота параллелограмма является так же и высотой
трапеции, так как основания
трапеции и
параллелограмма лежат на одних и тех же прямых (AB и DC).
Площадь трапеции:
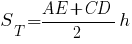
AE=AB/2 (по условию задачи).
AE=AB/2=CD/2 (по первому свойству параллелограмма).
Подставляем все полученные значения:
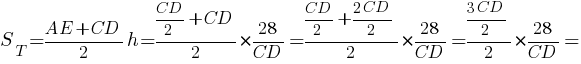
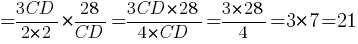
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
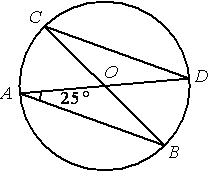 В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
 В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
 В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
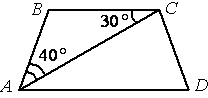 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.

Комментарии: