
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
 ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=7/9 (по первому
свойству биссектрисы).
Получаем, что:
AD/CD=7/9
AD=CD*7/9
И...
CD/BD=7/9
9CD=7BD
BD=CD*9/7
BD=AD+AB=AD+9+7=AD+16
AD+16=CD*9/7
Подставляем значение AD, которое получили ранее AD=CD*7/9
CD*7/9+16=CD*9/7
16=CD*9/7-CD*7/9
Приводим к общему знаменателю:
16=(9*9*CD-7*7*CD)/(7*9)
16=(81CD-49CD)/63
16*63=81CD-49CD
16*63=32CD
CD=16*63/32=63/2=31,5
Ответ: CD=31,5
Поделитесь решением
Присоединяйтесь к нам...
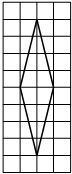 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
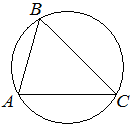 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√
Комментарии: