В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
Рассмотрим треугольник COD. Этот треугольник
равнобедренный, т.к. ОC и ОD - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /ODC=/OCD=80°.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=80°
Ответ: /OAB=80°.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
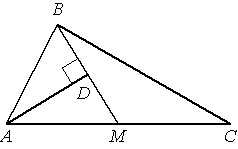Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
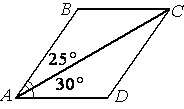Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: