
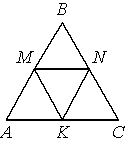
 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MN -
средняя линия треугольника ABC. Следовательно, MN=AK и MN||AK (по
теореме о средней линии).
NK - тоже
средняя линия, равна AM и параллельна AM.
Получается, что AM=MN=NK=KA, т.е. AMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
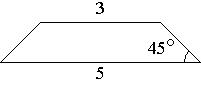 В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
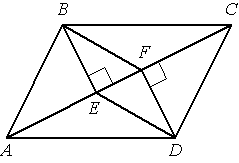 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Комментарии: