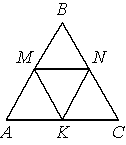
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
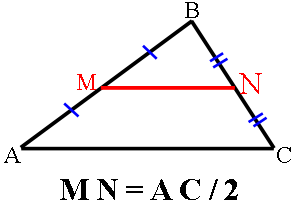
Тогда, MK -
средняя линия треугольника ABC. Следовательно, MK=BN и MK||BN (по
теореме о средней линии).
NK - тоже
средняя линия, равна BM и параллельна BM.
Получается, что MK=BN=BM=NK, т.е. BMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
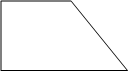Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: