
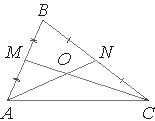
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. ON=AO/2
При этом AN=AO+ON
12=AO+ON, подставляем в это уравнение первое равенство:
12=AO+AO/2 |*2
24=2AO+AO
24=3AO
AO=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
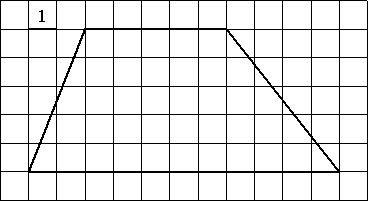 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
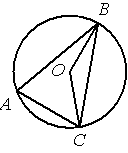 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
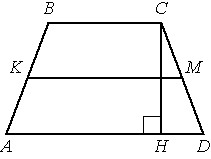 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
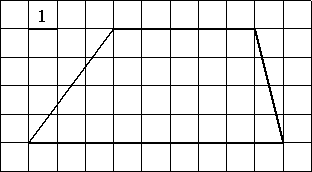 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
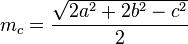 , где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон:
, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: 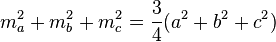
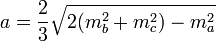 , где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
Комментарии:
(2019-06-06 10:47:20) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2019-06-06 09:29:24) : Точки м и н являются серединами сторон аб и бс треугольника абс соответственно отрезки ан см пересекаются в точке о ан 24 см 15 гайдиге ао
(2019-05-24 22:13:53) Администратор: Анна, к сожалению, такой информации у меня нет.
(2019-05-24 21:58:33) Анна : А это из 2-й части?
(2017-11-13 21:54:06) : Думаю, что просто задача составлена в общем виде. Т.е. условие будет использовано для нахождения различных величин. Для нахождения конкретно АО условия избыточны. К сожалению, это не редко встречается в задачах.
(2017-11-13 13:41:16) : почему использованы не все данные? например, зачем дано CM=18?