
 Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
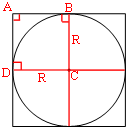 Проведем радиусы окружности к точкам касания со сторонами
квадрата, как показано на рисунке.
Проведем радиусы окружности к точкам касания со сторонами
квадрата, как показано на рисунке.
Обозначим ключевые точки A, B, C и D.
ABCD образует четырехугольник.
В этом четырехугольнике:
∠A=90° (по определению квадрата).
∠B=∠D=90° (по свойству касательной).
Тогда и ∠С=90° (так как сумма углов четырехугольника равна 360°).
Т.е. ABCD - прямоугольник (по
определению).
По свойству прямоугольника:
AB=CD=R
AD=BD=R
Т.е. ABCD - квадрат.
Из рисунка очевидно, что радиус равен половине стороны квадрата:
R=56/2=28
Ответ: 28
Поделитесь решением
Присоединяйтесь к нам...
 Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
 Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
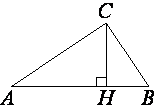 В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
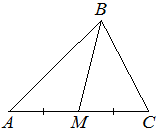 В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
Комментарии: