Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
По
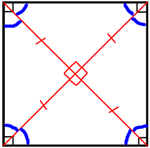
первому свойству квадрата, все его углы прямые, следовательно, треугольники, которые образует диагональ, прямоугольные.
Т.е. к этим треугольникам можно применить теорему Пифагора.
По определению квадрата, все его стороны равны, следовательно катеты этих треугольников равны:
d2=(9√2)2+(9√2)2
d2=2(9√2)2
По первому правилу действий со степенями:
d2=2*92(√2)2
d2=2*81*2=324
d=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна
722√
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
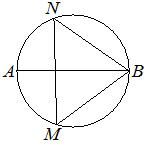На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: