
 Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
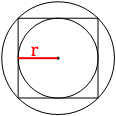 Проведем радиус
вписанной окружности, как на рисунке.
Проведем радиус
вписанной окружности, как на рисунке.
Очевидно, что r=a/2, где а - сторона
квадрата.
a=2r=2*24√2=48√2
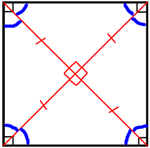
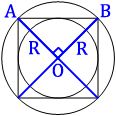 Проведем диаметры
описанной окружности, как показано на втором рисунке.
Проведем диаметры
описанной окружности, как показано на втором рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=OA2+OB2
a2=R2+R2
a2=2R2
(48√2)2=2R2
2304*2=2R2
2304=R2
R=√2304=48
Ответ: 48
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен 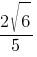 . Найдите sinA.
. Найдите sinA.
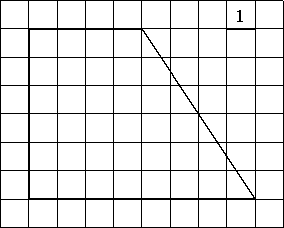 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
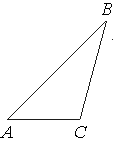 В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
Комментарии:
(2024-02-11 17:36:43) лена: ттт