
 Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
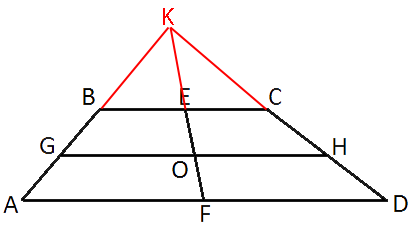 Продлим стороны AB и CD до пересечения в точке K.
Продлим стороны AB и CD до пересечения в точке K.
Рассмотрим треугольник AKD.
По
теореме о сумме углов треугольника:
∠AKD+∠KDA+∠DAK=180°
∠AKD+50°+40°=180°
∠AKD=90°
Следовательно треугольник AKD -
прямоугольный с гипотенузой AD.
KF -
медиана (по условию задачи).
Мысленно опишем вокруг этого треугольника окружность. Так как треугольник
прямоугольный, то центр окружности располагается на середине гипотенузы AD (по
теореме об описанной окружности).
Следовательно AF=FD=R - радиус окружности,
медиана KF тоже равна радиусу и, следовательно, равна AD/2.
Рассмотрим треугольник GKH.
Для этого треугольника KO -
медиана и равна половине гипотенузы GH (как и у предыдущего треугольника).
KO=OH=GH/2
В треугольнике BKC - аналогичная ситуация: KE=EC=BC/2
Вернемся к треугольнику GKH:
KO=OH=GH/2=15/2=7,5
7,5=OH=KE+EO=EC+EF/2
EC=7,5-EF/2=7,5-13/2=7,5-6,5=1
BC=2*EC=2*1=2
Рассмотрим трапецию ABCD.
GH -
средняя линия, следовательно GH=(BC+AD)/2
2GH=BC+AD
AD=2GH-BC=2*15-2=30-2=28
Ответ: AD=28, BC=2
Поделитесь решением
Присоединяйтесь к нам...
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
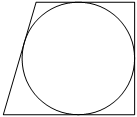 Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
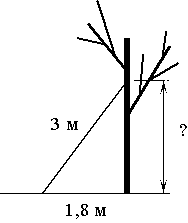 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Комментарии: