
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Решение прислал пользователь Людмила
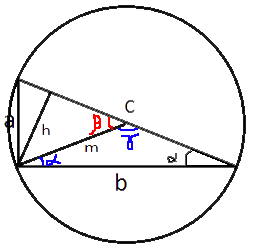 Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Если описать окружность вокруг треугольника, то центр этой окружности будет лежать на середине гипотенузы (по
теореме об описанной окружности). Следовательно:
m=c/2=20/2=10
S=(1/2)hc => h=2S/c=2*50√
По
определению синуса:
sinβ=h/m=5√
По таблице определяем, что β=45°
Угол γ является внешнем к β, следовательно γ=180°-β=180°-45°=135°
Треугольник, содержащий угол γ,
равнобедренный, так как медиана m и половина гипотенузы равны (это мы выяснили ранее).
Следовательно, по
свойству равнобедренного треугольника углы при основании равны (обозначены α).
Тогда, по
теореме о сумме углов треугольника:
180°=γ+α+α
180°=135°+2α
α=22,5° - это один из искомых углов.
Другой искомый угол найдем по той же
теореме об углах треугольника: 180°-90°-22,5°=67,5°
ответ: 22,5° и 67,5°
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
 Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
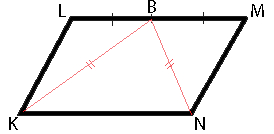 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
Комментарии: