
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ449 –Є–Ј 1087 |
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б—В–Њ—А–Њ–љ–∞ AB=32, AC=64, —В–Њ—З–Ї–∞ O вАФ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Я—А—П–Љ–∞—П BD, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞—П –њ—А—П–Љ–Њ–є AO, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г AC –≤ —В–Њ—З–Ї–µ D. –Э–∞–є–і–Є—В–µ CD.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Б—В–Њ—А–Њ–љ–∞ AB=32, AC=64, —В–Њ—З–Ї–∞ O вАФ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Я—А—П–Љ–∞—П BD, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞—П –њ—А—П–Љ–Њ–є AO, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г AC –≤ —В–Њ—З–Ї–µ D. –Э–∞–є–і–Є—В–µ CD.
–Я—А–Њ–≤–µ–і–µ–Љ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–є –Њ—В—А–µ–Ј–Њ–Ї –Є –≤–≤–µ–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ:
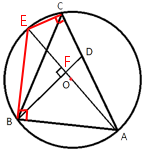 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AEB –Є AFB.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AEB –Є AFB.
∠BAE - –Њ–±—Й–Є–є
∠EBA=90¬∞, —В.–Ї. AE - –і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є (
—В–µ–Њ—А–µ–Љ–∞ –Њ–± –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є)
∠AFB=90¬∞, —В.–Ї. –њ–Њ —Г—Б–ї–Њ–≤–Є—О AD ⊥ AE
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л.
–Ґ–Њ–≥–і–∞:
AE/AB=AB/AF => AE*AF=AB2
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AEC –Є AFD.
∠FAD - –Њ–±—Й–Є–є
∠ACE=90¬∞, —В.–Ї. AE - –і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є (
—В–µ–Њ—А–µ–Љ–∞ –Њ–± –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є)
∠AFD=90¬∞, —В.–Ї. –њ–Њ —Г—Б–ї–Њ–≤–Є—О BD ⊥ AE
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л.
–Ґ–Њ–≥–і–∞:
AE/AD=AC/AF => AD=AE*AF/AC
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤—Л—И–µ –љ–∞–є–і–µ–љ–љ–Њ–µ —А–∞–≤–µ–љ—Б—В–≤–Њ:
AD=AB2/AC=322/64=16
CD=AC-AD=64-16=48
–Ю—В–≤–µ—В: CD=48
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O —А–∞–≤–µ–љ 29, –і–ї–Є–љ–∞ —Е–Њ—А–і—Л AB —А–∞–≤–љ–∞ 40 (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Е–Њ—А–і—Л AB –і–Њ –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ–є –µ–є –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є k.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O —А–∞–≤–µ–љ 29, –і–ї–Є–љ–∞ —Е–Њ—А–і—Л AB —А–∞–≤–љ–∞ 40 (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Е–Њ—А–і—Л AB –і–Њ –њ–∞—А–∞–ї–ї–µ–ї—М–љ–Њ–є –µ–є –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є k.
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 98√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 98√
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC BM вАУ –Љ–µ–і–Є–∞–љ–∞ –Є BH вАУ –≤—Л—Б–Њ—В–∞. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AC=84 –Є BC=BM. –Э–∞–є–і–Є—В–µ AH.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC BM вАУ –Љ–µ–і–Є–∞–љ–∞ –Є BH вАУ –≤—Л—Б–Њ—В–∞. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AC=84 –Є BC=BM. –Э–∞–є–і–Є—В–µ AH.
 –Ю—В—А–µ–Ј–Ї–Є AB –Є CD —П–≤–ї—П—О—В—Б—П —Е–Њ—А–і–∞–Љ–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і—Л CD, –µ—Б–ї–Є AB=20, CD=48, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і—Л AB —А–∞–≤–љ–Њ 24.
–Ю—В—А–µ–Ј–Ї–Є AB –Є CD —П–≤–ї—П—О—В—Б—П —Е–Њ—А–і–∞–Љ–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і—Л CD, –µ—Б–ї–Є AB=20, CD=48, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і—Л AB —А–∞–≤–љ–Њ 24.
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 6.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 6.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-05-20 00:10:22) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: Alissa, –і–∞, —Н—В–Њ –Њ–њ–µ—З–∞—В–Ї–∞, —Б–њ–∞—Б–Є–±–Њ, —З—В–Њ –Њ–±–љ–∞—А—Г–ґ–Є–ї–Є. –Ш—Б–њ—А–∞–≤–ї–µ–љ–Њ!
(2017-05-19 19:24:30) Alissa: –Т —А–µ—И–µ–љ–Є–Є –Ј–∞–і–∞—З–Є –µ—Б—В—М —В–∞–Ї–∞—П –Ј–∞–њ–Є—Б—М\"∠AFB=90¬∞, —В.–Ї. –њ–Њ —Г—Б–ї–Њ–≤–Є—О AD ⊥ AE\". –Я–Њ—З–µ–Љ—Г \"AD ⊥ AE\"?–£ –≤–∞—Б –Њ–њ–µ—З–∞—В–Ї–∞ \"–ТD ⊥ AE\"
(2017-05-17 22:39:41) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ы–µ—А–∞, –Р–Х - —Н—В–Њ –і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –ї—О–±–Њ–є –≤–њ–Є—Б–∞–љ–љ—Л–є —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ –Р–Х –±—Г–і–µ—В –њ—А—П–Љ—Л–Љ. –Я–Њ—Н—В–Њ–Љ—Г –Х–Т –≤—Б–µ–≥–і–∞ –±—Г–і–µ—В –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ –Р–Т.
(2017-05-17 21:33:21) –Ы–µ—А–∞: –Х—Б–ї–Є –љ–∞—З–µ—А—В–Є—В—М –і—А—Г–≥–Њ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —В–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Є–Ј —В–Њ—З–Ї–Є –Х –љ–µ –±—Г–і—Г—В –Њ–њ—Г—Б–Ї–∞—В—М—Б—П –≤ —В–Њ—З–Ї—Г –Т, –Ј–љ–∞—З–Є—В —В–∞–Ї –Ј–∞–і–∞—З–∞ –љ–µ —А–µ—И–Є—В—Б—П
(2017-02-01 15:25:29) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р—Б—П, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –њ–Є—И–Є—В–µ, –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2017-01-31 18:01:19) –Р—Б—П: –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞—Е ABE –Є KMP –Є–Ј–≤–µ—Б—В–љ—Л —Б—В–Њ—А–Њ–љ—Л: AB=3,BE=5,AE=7.MP=15,PK=21 –љ–Р–Щ–Ф–Ш–Ґ–Х –Ф–Ы–Ш–Э–£ –°–Ґ–Ю–†–Ю–Э–Ђ mk –Х–°–Ы–Ш —Г–≥–Њ–ї P= —Г–≥–ї—Г E