Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Так как AC проходит через центр окружности, значит это диаметр.
Треугольник ABC вписан в окружность и центр окружности лежит на середине AC, следовательно треугольник ABC
прямоугольный с гипотенузой AC(по
теореме об описанной окружности).
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=30°+90°+∠C
∠C=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
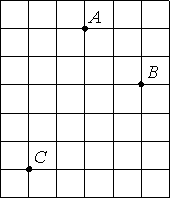На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
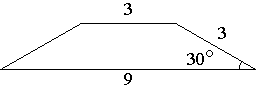Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 21:48:02) Алина: Потому что ∠ABC прямоугольный =90°
(2014-05-26 18:48:07) мариша: Откуда взяли 90°?
(2014-05-19 13:03:26) ольга: можно еще через дуги. дуга bc=60 т.к. ac диаметр ,то 360:2=180 значит дуга ab=120 и т.к. <с=1/2 дуги ab, то <с=60
(2014-05-18 12:58:49) Ирина: все понятно спасибо