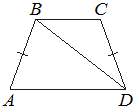
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Трапеция ABCD
равнобедренная, так как AB=CD.
Следовательно, по второму свойству равнобедренной трапеции:
∠BAD=∠CDA=∠BDA+∠BDC=38°+32°=70°
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника:
180°=∠BAD+∠BDA+∠ABD
180°=70°+38°+∠ABD
∠ABD=180°-70°-38°=72°
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
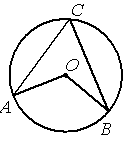Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
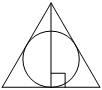Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
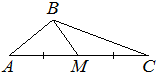В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: