
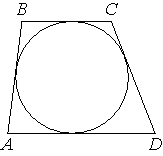 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Так как в трапецию вписана
окружность, то:
AD+BC=AВ+CD (по четвертому свойству трапеции).
AD+13=14+22
AD=14+22-13=23
Ответ: 23
Поделитесь решением
Присоединяйтесь к нам...
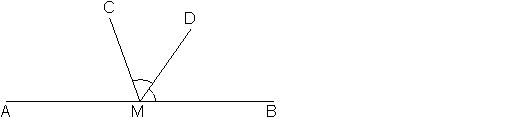 На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
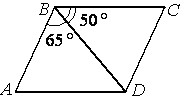 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии:
(2019-12-25 08:18:36) С.: трапеция абсд с основаниями ад и бс вписана в окружность. так,что ад-диаметр окружности .Диагональ трапеции равна 10 см,а её площадь - 25см2.