
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ828 –ł–∑ 1087 |
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AD=4, BC=3, –į –Ķ—Ď –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–į–≤–Ĺ–į 84. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM, –≥–ī–Ķ MN ‚ÄĒ —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AD=4, BC=3, –į –Ķ—Ď –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–į–≤–Ĺ–į 84. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM, –≥–ī–Ķ MN ‚ÄĒ —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD.
–ü–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł –≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ: –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ—É—Ā—É–ľ–ľ—č –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ļ –ł –≤—č—Ā–ĺ—ā—č.
–Ę.–Ķ. –ī–Ľ—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ľ–ĺ–∂–Ķ–ľ –∑–į–Ņ–ł—Ā–į—ā—Ć:
SABCD=h*(AD+BC)/2
84=h*(4+3)/2
168=7h
h=24
–Ē–Ľ—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM:
SBCNM=hBCNM*(MN+BC)/2
MN - —ć—ā–ĺ —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź, –∑–Ĺ–į—á–ł—ā –ī–Ľ–ł–Ĺ–į —Ä–į–≤–Ĺ–į –Ņ–ĺ–Ľ—É—Ā—É–ľ–ľ–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ļ:
MN=(AD+BC)/2=(4+3)/2=3,5
–í—č—Ā–ĺ—ā–į —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM —Ä–į–≤–Ĺ–į –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ķ –≤—č—Ā–ĺ—ā—č —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD (–Ņ–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –§–į–Ľ–Ķ—Ā–į), —ā–ĺ–≥–ī–į:
SBCNM=hBCNM*(MN+BC)/2=(h/2)*(3,5+BC)/2=(24/2)*(3,5+3)/2=12*3,25=39
–ě—ā–≤–Ķ—ā: 39
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 22, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
–°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 22, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
 –°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 32, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
–°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 32, –į –ĺ—Ā—ā—Ä—č–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 60¬į. –í—č—Ā–ĺ—ā–į —Ä–ĺ–ľ–Ī–į, –ĺ–Ņ—É—Č–Ķ–Ĺ–Ĺ–į—Ź –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č —ā—É–Ņ–ĺ–≥–ĺ —É–≥–Ľ–į, –ī–Ķ–Ľ–ł—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É –Ĺ–į –ī–≤–į –ĺ—ā—Ä–Ķ–∑–ļ–į. –ö–į–ļ–ĺ–≤—č –ī–Ľ–ł–Ĺ—č —ć—ā–ł—Ö –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤?
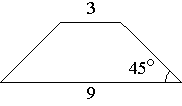 –í —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č 3 –ł 9, –į –ĺ–ī–ł–Ĺ –ł–∑ —É–≥–Ľ–ĺ–≤ –ľ–Ķ–∂–ī—É –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ –ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–í —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č 3 –ł 9, –į –ĺ–ī–ł–Ĺ –ł–∑ —É–≥–Ľ–ĺ–≤ –ľ–Ķ–∂–ī—É –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ –ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ä–į–≤–Ķ–Ĺ 45¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ—č —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č M –ł N —Ā—ā–ĺ—Ä–ĺ–Ĺ BC –ł AC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ü–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į CNM —Ä–į–≤–Ĺ–į 67. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABMN.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ—č —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č M –ł N —Ā—ā–ĺ—Ä–ĺ–Ĺ BC –ł AC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ü–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į CNM —Ä–į–≤–Ĺ–į 67. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABMN.
 –Ď–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 10, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ 12. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–Ď–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 10, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ 12. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.

 , –ł–Ľ–ł
, –ł–Ľ–ł  , –≥–ī–Ķ m - —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
, –≥–ī–Ķ m - —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: