Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=5/15=1/3
BD/AD=15/45=1/3
Тогда по
второму признаку подобия треугольников, треугольники CBD и ADB подобны.
Поделитесь решением
Присоединяйтесь к нам...
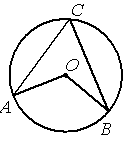Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
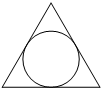Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
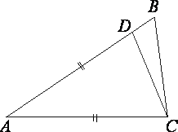Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: