Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
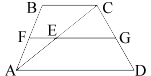Обозначим ключевые точки, как показано на рисунке.
Рассмотрим треугольник ABC.
AF=FB (по
определению средней линии трапеции).
Тогда, по теореме Фалеса:
AE=EC
Получается, что FE -
средняя линия треугольника ABC.
FE=BC/2=8/2=4 (по
теореме о средней линии треугольника).
Рассмотрим треугольник ACD.
Аналогично, EG -
средняя линия данного треугольника, следовательно EG=AD/2=18/2=9.
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
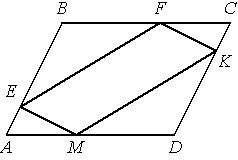В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Площадь прямоугольного треугольника равна 2450√
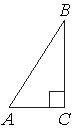В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.
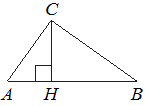На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: