В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Площадь
трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции.
hтр*(3+1)/2=12 (по условию задачи)
h=12/2=6
Проведем
высоту треугольника ABC, как показано на рисунке.
hтреугольника=hтр, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и образуют прямоугольник.
Sтреугольника=hтреугольника*BC/2=6*1/2=3
Ответ: Sтреугольника=3
Поделитесь решением
Присоединяйтесь к нам...
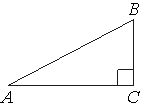В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
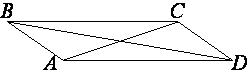В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
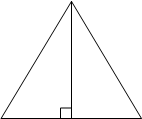Высота равностороннего треугольника равна 96√
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
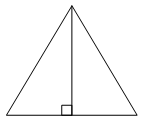Высота равностороннего треугольника равна 15√
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: