В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=30
По
определению средней линии трапеции: m=(BC+AD)/2=30/2=15
Ответ: m=15
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
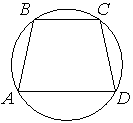Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: