
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ441 –Є–Ј 1087 |
 –Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О, –њ–µ—А–Є–Љ–µ—В—А –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–µ–љ 200, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 2000, –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —В—А–∞–њ–µ—Ж–Є–Є –і–Њ –µ—С –Љ–µ–љ—М—И–µ–≥–Њ –Њ—Б–љ–Њ–≤–∞–љ–Є—П.
–Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О, –њ–µ—А–Є–Љ–µ—В—А –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–µ–љ 200, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 2000, –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —В—А–∞–њ–µ—Ж–Є–Є –і–Њ –µ—С –Љ–µ–љ—М—И–µ–≥–Њ –Њ—Б–љ–Њ–≤–∞–љ–Є—П.
SABCD=EF*(AD+BC)/2=2000
PABCD=AB+BC+CD+AD=200
AB=CD (—В–∞–Ї –Ї–∞–Ї
—В—А–∞–њ–µ—Ж–Є—П —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–∞—П).
–І—В–Њ–±—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –≤–њ–Є—Б–∞—В—М –≤ —В—А–∞–њ–µ—Ж–Є—О –і–Њ–ї–ґ–љ–Њ –≤—Л–њ–Њ–ї–љ—П—В—М—Б—П —Г—Б–ї–Њ–≤–Є–µ - —Б—Г–Љ–Љ—Л –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л—Е —Б—В–Њ—А–Њ–љ —В—А–∞–њ–µ—Ж–Є–Є –і–Њ–ї–ґ–љ—Л –±—Л—В—М —А–∞–≤–љ—Л, —В.–µ.
AD+BC=AB+CD
AD+BC=2AB (—В.–Ї. AB=CD)
–Ґ–Њ–≥–і–∞:
PABCD=AB+BC+CD+AD=AB+2AB+AB=4AB=200
AB=50
–Ч–љ–∞—З–Є—В, AD+BC=2*50=100
SABCD=EF*(AD+BC)/2=EF*100/2=EF*50=2000
EF=40
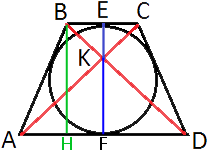 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г BH, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г BH, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
BH=EF=40, —В–∞–Ї –Ї–∞–Ї BEFH -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
AH=(AD-BC)/2
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=BH2+AH2
502=402+AH2
2500=1600+AH2
900=AH2
30=AH=(AD-BC)/2
60=AD-BC, –≤—Б–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ AD+BC=100
60=AD-(100-AD)
60=AD-100+AD
160=2AD
AD=80
–Ґ–Њ–≥–і–∞ BC=100-80=20
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AKF –Є CKE
AF=AD/2=40
CE=BC/2=10
∠AFK=∠CEK=90¬∞
∠AKF=∠CKE (—В.–Ї. –Њ–љ–Є
–≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ)
–Я–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л.
–Ґ–Њ–≥–і–∞, AF/CE=KF/KE
40/10=KF/KE
4=(EF-KE)/KE (–≤—Б–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ EF=40)
4KE=40-KE
5KE=40
KE=8
–Ю—В–≤–µ—В: KE=8
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
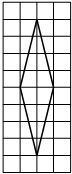 –Э–∞ –Ї–ї–µ—В—З–∞—В–Њ–є –±—Г–Љ–∞–≥–µ —Б —А–∞–Ј–Љ–µ—А–Њ–Љ –Ї–ї–µ—В–Ї–Є 1x1 –Є–Ј–Њ–±—А–∞–ґ—С–љ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —А–Њ–Љ–±–∞.
–Э–∞ –Ї–ї–µ—В—З–∞—В–Њ–є –±—Г–Љ–∞–≥–µ —Б —А–∞–Ј–Љ–µ—А–Њ–Љ –Ї–ї–µ—В–Ї–Є 1x1 –Є–Ј–Њ–±—А–∞–ґ—С–љ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —А–Њ–Љ–±–∞.
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=177¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=177¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 45¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 30¬∞ –Є 45¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
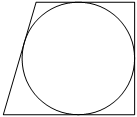 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 18. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Г—О —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 18. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
 –•–Њ—А–і—Л AC –Є BD –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ P, BP=9, CP=15, DP=20. –Э–∞–є–і–Є—В–µ AP.
–•–Њ—А–і—Л AC –Є BD –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ P, BP=9, CP=15, DP=20. –Э–∞–є–і–Є—В–µ AP.

 , –Є–ї–Є
, –Є–ї–Є  , –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
, –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: