
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ432 –Є–Ј 1087 |
 –Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 4 –Є 64, BD=16. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є ADB –њ–Њ–і–Њ–±–љ—Л.
–Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 4 –Є 64, BD=16. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є ADB –њ–Њ–і–Њ–±–љ—Л.
ABCD -
—В—А–∞–њ–µ—Ж–Є—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AD||BC.
∠CBD=∠ADB (—В.–Ї. —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В-–ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л –і–ї—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е AD –Є BC).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Њ—В–љ–Њ—И–µ–љ–Є—П —Б—В–Њ—А–Њ–љ:
BC/BD=4/16=1/4
BD/AD=16/64=1/4
–Ґ–Њ–≥–і–∞ –њ–Њ
–≤—В–Њ—А–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є ADB –њ–Њ–і–Њ–±–љ—Л.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
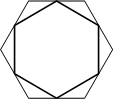 –Ф–∞–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –µ—Б–ї–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Б–Њ–µ–і–Є–љ–Є—В—М –Њ—В—А–µ–Ј–Ї–∞–Љ–Є —Б–µ—А–µ–і–Є–љ—Л –µ–≥–Њ —Б—В–Њ—А–Њ–љ, —В–Њ –њ–Њ–ї—Г—З–Є—В—Б—П –њ—А–∞–≤–Є–ї—М–љ—Л–є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї.
–Ф–∞–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –µ—Б–ї–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Б–Њ–µ–і–Є–љ–Є—В—М –Њ—В—А–µ–Ј–Ї–∞–Љ–Є —Б–µ—А–µ–і–Є–љ—Л –µ–≥–Њ —Б—В–Њ—А–Њ–љ, —В–Њ –њ–Њ–ї—Г—З–Є—В—Б—П –њ—А–∞–≤–Є–ї—М–љ—Л–є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC AB=BC=37, AC=24. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Љ–µ–і–Є–∞–љ—Л BM.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC AB=BC=37, AC=24. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Љ–µ–і–Є–∞–љ—Л BM.
 –Ю—В—А–µ–Ј–Ї–Є AB –Є CD —П–≤–ї—П—О—В—Б—П —Е–Њ—А–і–∞–Љ–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л CD, –µ—Б–ї–Є AB=20, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і AB –Є CD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 24 –Є 10.
–Ю—В—А–µ–Ј–Ї–Є AB –Є CD —П–≤–ї—П—О—В—Б—П —Е–Њ—А–і–∞–Љ–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л CD, –µ—Б–ї–Є AB=20, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Е–Њ—А–і AB –Є CD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 24 –Є 10.
–Ю—Б–љ–Њ–≤–∞–љ–Є–µ AC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–Њ 6. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —А–∞–і–Є—Г—Б–∞ 4,5 —Б —Ж–µ–љ—В—А–Њ–Љ –≤–љ–µ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ї–∞—Б–∞–µ—В—Б—П –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є—П –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Є –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є—П AC –≤ –µ–≥–Њ —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
–Э–∞ –Ї–∞–Ї–Њ–є —Г–≥–Њ–ї (–≤ –≥—А–∞–і—Г—Б–∞—Е) –њ–Њ–≤–Њ—А–∞—З–Є–≤–∞–µ—В—Б—П –Љ–Є–љ—Г—В–љ–∞—П —Б—В—А–µ–ї–Ї–∞, –њ–Њ–Ї–∞ —З–∞—Б–Њ–≤–∞—П –њ–Њ–≤–Њ—А–∞—З–Є–≤–∞–µ—В—Б—П –љ–∞ 14¬∞?

 , –Є–ї–Є
, –Є–ї–Є  , –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
, –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2019-03-22 19:41:52) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –Њ—В–њ—А–∞–≤—М—В–µ –Ј–∞—П–≤–Ї—Г –љ–∞ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –Ј–∞–і–∞—З–Є, –Є –Љ—Л –µ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2019-03-21 11:46:08) : –Њ—Б–љ–Њ–≤–∞–љ–Є–µ bc –Є ad —В—А–∞–њ–µ—Ж–Є–Є abcd —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 2 –Є 32 BD=8 –Ф–Ю–Ъ–Р–Ц–Ш–Ґ–Х –І–Ґ–Ю –Ґ–†–Х–£–У–Ю–Ы–ђ–Э–Ш–Ъ–Ш –°BD –Є BDA –њ–Њ–і–Њ–±–љ—Л
(2016-02-24 20:57:13) –Э–Є–Ї–Є—В–∞: –°–∞–є—В –њ—А–Њ—Б—В–Њ —Б—Г–њ–µ—А, –Њ—З–µ–љ—М –њ–Њ–Љ–Њ–≥–∞–µ—В !!!