
 В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
Обратите внимание, рисунок не соответствует условию задачи (углы на рисунке заведомо меньше, чем в условии).
/ADC=/BDA+/BDC=67°+28°=95°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, /BAD=/ADC=95°.
Сумма углов любого выпуклого n-угольника равна 180°*(n-2).
Тогда сумма углов трапеции равна 180°*(4-2)=360°, следовательно /ABC+/BCD=360°-95°-95°=170°
По тому же
свойству равнобедренной трапеции /ABC=/BCD, тогда каждый из этих углов равен 170°/2=85°
В любой трапеции основания параллельны (по
определению), т.е. AD||BC, тогда, рассматривая BD как секущую, заметим, что /CBD=/BDA=67° (т.к. это
внутренние накрест лежащие углы).
Тогда /ABD=/ABC-/CBD=85°-67°=18°
Ответ: /ABD=18°
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
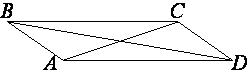 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
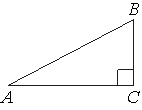 В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
 В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии: