Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
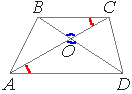Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда:
∠DAO=∠BCO (накрест лежащие углы).
∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
15/11=AO/OC
15*OC=11*AO
При этом AO+OC=AC=52
OC=52-AO, подставляем это равенство в ранее полученную пропорцию:
15*(52-AO)=11*AO
780-15*AO=11*AO
780=15*AO+11*AO
780=26*AO
AO=780/26=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
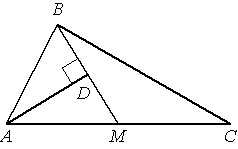Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
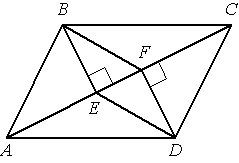В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: