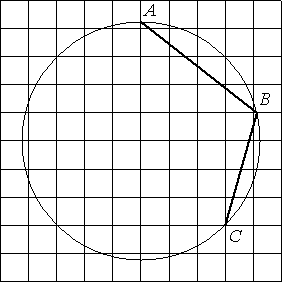
Найдите угол ABC. Ответ дайте в градусах.
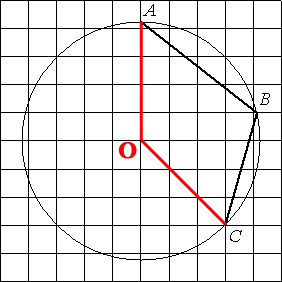Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается (ABC), тоже равна 135°.
Следовательно, бОльшая дуга имеет градусную меру 360°-135°=225°
∠ABC -
вписанный угол, опирается на бОльшую дугу и по
теореме равен 225°/2=112,5°
Ответ: 112,5
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
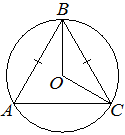Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
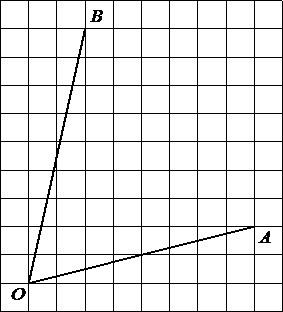Найдите тангенс угла
AOB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: