
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
 ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=3/12 (по первому
свойству биссектрисы).
Из этих равенств выписываем:
AD=CD*3/12
BD=CD*12/3=4CD, (BD=AD+AB=AD+12+3=AD+15)
AD+15=4CD
CD*3/12+15=4CD
15=4CD-CD*3/12=4CD-CD/4
15=(16CD-CD)/4
15*4=15CD
CD=4
Ответ: CD=4
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
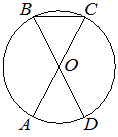 В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
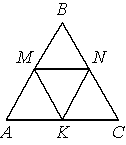 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Комментарии:
(2014-05-29 15:56:34) НЯня: Спасибочки!!