Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Так как треугольник ABC
равнобедренный, то:
∠BAC=∠BCA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠BAC+∠BCA+∠ABC
180°=x+x+79°
101°=2x
x=50,5°=∠BAC
∠BAC -
вписанный в окружность угол, следовательно градусная мера дуги, на которую он опирается (дуга BC) вдвое больше самого угла:
2*50,5°=101°
∠BOC -
центральный угол, следовательно, он равен градусной мере дуги, на которую он опирается, т.е. 101°
Ответ: 101
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
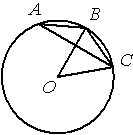Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-21 09:50:57) Дурак: Спасибо, всё правильно.