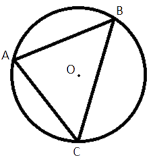Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Градусная мера всей окружности 360°.
Разделим ее на равные условные части так, чтобы одна дуга имела 3 такие части, вторая дуга 7 частей, а третья 8 частей (как у условии задачи). Тогда понятно, что нам нужно 3+7+8 таких частей, итого 18.
Градусная мера каждой части равна 360°/18=20°.
Тогда наша первая дуга имеет градусную меру 20°*3=60°, вторая - 20°*7=140°, третья - 20°*8=160°.
Углы ABC, BCA и CAB -
вписанные в окружность, следовательно, они равны половине градусной меры дуги, на которую опираются, т.е.:
Один угол равен 30°, второй 70°, а третий 80°.
По
теореме о соотношении углов и сторон треугольника: на против меньшей стороны лежит меньший угол. Меньший угол равен 30° (это мы только что вычислили), а меньшая сторона равна 20 (по условию задачи).
По
теореме синусов 20/sin30°=2R
20/0,5=2R
40=2R
R=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
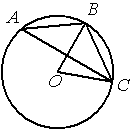Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
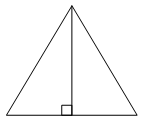Высота равностороннего треугольника равна 78√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: