Найдите угол ABC . Ответ дайте в градусах.
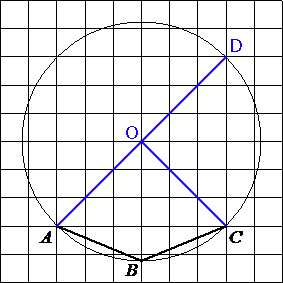Проведем отрезки как показано на рисунке.
∠AOC -
центральный угол.
По рисунку (по клеточкам) видно, что ∠AOC=90°
Следовательно дуга ABC=90°
Тогда дуга ADC=360°-90°=270°
∠ABC опирается на эту дугу ADC и является
вписанным, по
теореме о вписанном угле:
∠ABC=270°/2=135°
Ответ: 135
Поделитесь решением
Присоединяйтесь к нам...
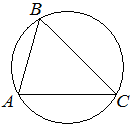В треугольнике ABC угол C равен 45°, AB=6√
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-06 22:54:44) Администратор: Елена, тоже вариант...
(2015-04-06 22:20:14) Елена: По сетке чётко видно, что АВС - это часть вписанного в окружность правильного восьмиугольника. Угол АВС - угол правильного восьмиугольника. Он равен 180*(8-2)/8=135