
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 47°*2=94°.
Тогда дуга NB равна 180°-94°=86°
/NMB - тоже
вписанный в окружность, следовательно он равен 86°/2=43°
Ответ: 43
Поделитесь решением
Присоединяйтесь к нам...
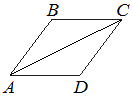 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
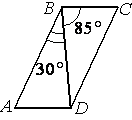 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
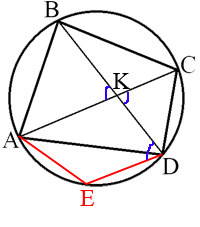 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
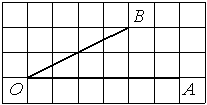 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
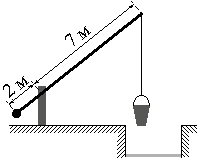 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?

Комментарии: