На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 38°*2=76°.
Тогда дуга NB равна 180°-76°=104°
/NMB - тоже
вписанный в окружность, следовательно он равен 104°/2=52°
Ответ: /NMB=52°
Поделитесь решением
Присоединяйтесь к нам...
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
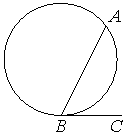На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-11 22:25:48) Администратор: Вика, нет, ответ 52 градуса (Вы ошиблись, задан угол не в 36, а в 38 градусов. А впринципе Вы правы, можно решать и так. Только придется указывать, что треугольник прямоугольный потому-то, потому-то. Оба угла вписанные, поэтому равны и т.д. Мне кажется, что Ваше решение подходит для учащихся на хорошем уровне, мое же понятней для всех. Но все равно спасибо за преложенный вариант.
(2017-02-11 19:46:28) вика: А разве ответ не 54 градусов?! ANB= 90градусов и 90-36=54 не проще ли?
(2016-10-06 18:33:06) Администратор: Посмотрите задачу 767, она очень похожа на Вашу.
(2016-10-06 18:08:23) : основание трапеции равны 1 и 17 найти больший из отрезков на которое делит среднюю линию этой трапеции одна из ее диогоналей
(2015-05-19 21:20:21) Администратор: Софья, конечно 104/2, спасибо, что нашли опечатку. Исправлено.
(2015-05-19 18:21:14) Cофья: Извините, а не 104:2?
(2015-05-17 23:49:03) Администратор: 38°*2=76° (по теореме о вписанном угле).
(2015-05-17 16:12:40) Роман: а каким образом AN=76 градусов?