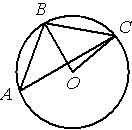
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=40°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 40°*2=80°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=80°.
Ответ: /BOC=80°.
Поделитесь решением
Присоединяйтесь к нам...
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Катеты прямоугольного треугольника равны 4√
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: