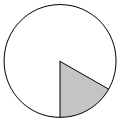
Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Центральный угол равен 60°, следовательно, градусная мера дуги, на которую он опирается, тоже равна 60°.
Градусная мера всего круга равна 360°.
Следовательно, площадь сектора составляет 60°/360°=1/6 часть от площади круга.
Тогда, площадь сектора равна 78/6=13.
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Площадь прямоугольного треугольника равна 50√
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: