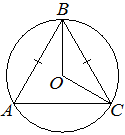Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Так как треугольник ABC
равнобедренный, то:
∠BAC=∠BCA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠BAC+∠BCA+∠ABC
180°=x+x+57°
180°-57°=2x
123°=2x
x=123°/2=61,5°=∠BAC
∠BAC -
вписанный в окружность угол, следовательно градусная мера дуги, на которую он опирается (дуга BC) вдвое больше самого угла:
2*61,5°=123°
∠BOC -
центральный угол, следовательно, он равен градусной мере дуги, на которую он опирается, т.е. 123°
Ответ: 123
Поделитесь решением
Присоединяйтесь к нам...
Площадь равнобедренного треугольника равна 1600√
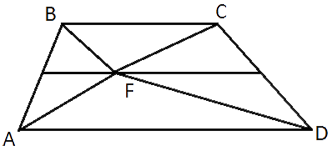На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
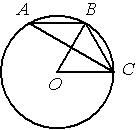Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: