
 Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
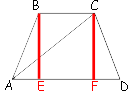 Обозначим ключевые точки, как показано на рисунке и проведем
высоты BE и CF.
Обозначим ключевые точки, как показано на рисунке и проведем
высоты BE и CF.
Рассмотрим четырехугольник BCFE.
∠CFE=∠BEF=90° (так как BE и CF -
высоты).
∠CBE=180°-∠BEF=180°-90°=90° (так как это
внутренние односторонние углы при параллельных прямых AD и BC и секущей BE).
∠BCF=90° (аналогично углу CBE).
Получается, что BCFE -
прямоугольник.
Тогда BE=CF и BC=EF=3 (по
свойству прямоугольника).
Рассмотрим треугольники ABE и CDF.
AB=CD=25 (так как
трапеция равнобедренная).
BE=CF (это мы выяснили ранее).
∠ABC=∠DCB (так как по
свойству равнобедренной трапеции, угли при одном основании равны).
Следовательно, равно и следующее равенство:
∠ABC-90°=∠DCB-90° - это и есть углы ABE и DCF соответственно, т.е.:
∠ABE=∠DCF
Тогда, по
второму признаку равенства треугольников, данные треугольники равны.
Следовательно, AE=FD.
AD=AE+EF+FD=AE+BC+AE=2AE+3=17
2AE=14
AE=7=FD
Найдем
высоту CF по
теореме Пифагора:
CD2=CF2+FD2
252+CF2+72
625=CF2+49
CF2=576
CF=24
Найдем AC по
теореме Пифагора:
AC2=CF2+AF2
AC2=CF2+(AE+EF)2
AC2=242+(7+3)2
AC2=576+100=676
AC=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
 Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
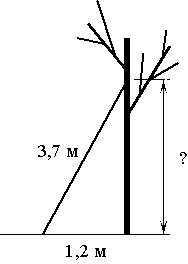 Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

Комментарии: