
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Вариант №1 (Прислал один из наших пользователей, имя не известно).
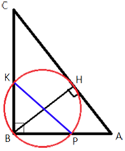 ∠KBP=90° (по условию)
∠KBP=90° (по условию)
Прямоугольный треугольник KPB с гипотенузой PK вписан в окружность.
Следовательно, PK является диаметром окружности. (по
теореме об описанной окружности).
KP=BH=16
Ответ: PK=16
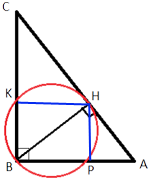 Проведем отрезки KH и HP.
Проведем отрезки KH и HP.Поделитесь решением
Присоединяйтесь к нам...
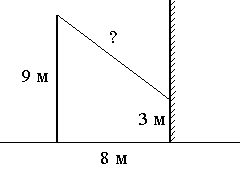 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
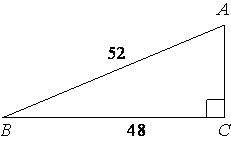 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
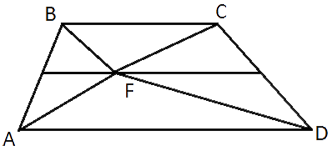 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.

Комментарии: