Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Рассмотрим каждое утверждение:
1) "Медиана
равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам", это утверждение верно (по
свойству равнобедренного треугольника).
2) "Не существует прямоугольника, диагонали которого взаимно перпендикулярны", это утверждение неверно,
квадрат - такой
прямоугольник.
3) "В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса", это утверждение верно. Это очевидно, если провести отрезок через центр
окружности и данную точку, радиус будет меньше этого отрезка.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Найдите площадь треугольника, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
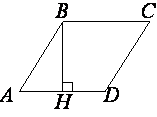Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-10 22:30:29) Администратор: Нет, конечно. Смежные углы характерны тем, что их сумма равна 180 градусов. А вот вертикальные углы равны.
(2017-01-10 19:47:24) : смежные углы равны?