
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
∠CBA - является
смежным внешнему углу, следовательно, 180°=∠CBA+155°
∠CBA=180°-155°=25°
Так как AC=BC, то треугольник ABC -
равнобедренный.
Значит ∠CBA=∠CAB=25° (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=25°+25°+∠C
∠C=130°
Ответ: 130
Поделитесь решением
Присоединяйтесь к нам...
 Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
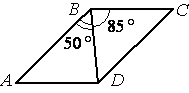 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
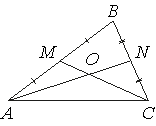 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
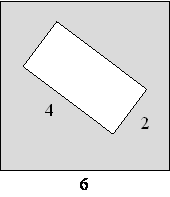 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Комментарии: