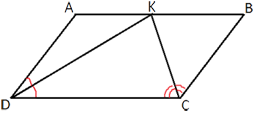Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
∠CDK=∠AKD (т.к. это
накрест-лежащие углы).
Так как DK -
биссектриса, то:
∠CDK=∠ADK.
Получается, что треугольник AKD -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда, по
определению равнобедренного треугольника:
AD=AK.
∠DCK=∠CKB (т.к. это
накрест-лежащие углы).
Так как CK -
биссектриса, то:
∠DCK=∠KCB.
Получается, что треугольник CKB -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда, по
определению равнобедренного треугольника:
BC=BK.
AD=BC (по
свойству
параллелограмма), следовательно:
AK=KB
Поделитесь решением
Присоединяйтесь к нам...
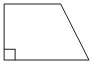Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
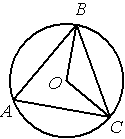Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-02-25 20:24:08) Администратор: da13, не за что)
(2018-02-25 20:18:43) da13: Я поняла) СПасибо!
(2018-02-25 20:16:38) da13: Почему СК - биссектриса?
(2016-09-22 15:59:07) Администратор: Карина, мы не помогаем делать домашнее задание, а разбираем задачи, которые будут на экзаменах. Эти задачи берутся с сайта fipi.ru.
(2016-09-22 15:30:19) карина: ав=сд ас=ад доказать что параллелограмм